ソーシャルゲームにおけるガチャの排出確率について考える

目次
ソーシャルゲームにおけるガチャの排出確率とその影響について
ソーシャルゲームにおけるガチャは、プレイヤーがゲーム内アイテムやキャラクターを入手するための重要な仕組みです。
ガチャの排出確率はプレイヤーの行動やゲームの収益に大きな影響を与えます。
例えば、レアなアイテムの排出確率が低いと、プレイヤーはより多くのガチャを引くために課金を行う可能性が高まります。
これにより、ゲームの収益が増加する一方で、プレイヤーの満足度やゲームバランスにも影響が出ることがあります。
ガチャの排出確率を理解することは、プレイヤーにとっても重要であり、ゲーム運営側がプレイヤーの信頼を維持するためにも透明性が求められます。
ガチャの仕組みと基本的な確率の理解
ガチャの仕組みは基本的にはランダムな抽選に基づいており、特定のアイテムが排出される確率が設定されています。
この確率は通常、運営側によって事前に決められています。
例えば、レアキャラクターの排出確率が1%で設定されている場合、100回ガチャを引いても必ずしも1回当たるわけではありません。
このような確率の基本的な理解は、プレイヤーがガチャを引く際の期待値や運営側が設定する確率の妥当性を評価するために重要です。
ガチャ排出確率がゲームに与える影響とプレイヤーの行動
ガチャの排出確率が低いと、プレイヤーは目的のアイテムを入手するために多額の課金を行うことがあります。
これはゲームの収益を大幅に増加させる一方で、一部のプレイヤーにとっては不満やストレスの原因となることがあります。
さらに、ガチャの排出確率が不透明である場合、プレイヤーの信頼を損ね、ゲームの評判にも悪影響を与える可能性があります。
確率に基づくガチャ戦略とその実例
プレイヤーは、ガチャの確率を理解した上で、効率的な戦略を立てることが重要です。
例えば、特定のイベント期間中に確率が上昇するガチャを狙ったり、確率が低い場合には複数回引くことで期待値を上げる戦略を取ることが考えられます。
実際のゲームにおいても、このような戦略を活用するプレイヤーが多く見受けられます。
プレイヤー心理に与えるガチャの確率と期待値
ガチャの確率と期待値は、プレイヤーの心理にも大きな影響を与えます。
高い期待値を持つガチャはプレイヤーのモチベーションを高め、ゲームへの没入感を強化します。
一方で、低い確率や不透明なガチャは、プレイヤーの不満や退屈感を引き起こす可能性があります。
そのため、運営側は適切な確率設定と透明性の確保が求められます。
ガチャ排出確率の透明性とその重要性
ガチャの排出確率を公開することは、プレイヤーの信頼を維持するために非常に重要です。
多くのゲームでは、ガチャの確率を公式サイトやゲーム内で公開することで、プレイヤーが安心してゲームを楽しめるようにしています。
透明性のある確率設定は、長期的に見てゲームの成功に貢献します。
Pythonで二項分布を使ったガチャの排出確率の可視化方法
Pythonを使ってガチャの排出確率を可視化する方法は、プログラミング初心者でも理解しやすい手順で進めることができます。
二項分布を用いることで、ガチャをN回まわしたときに特定の結果が出る確率を計算できます。
これは、Pythonの標準ライブラリである`scipy.stats`を使うことで簡単に実現できます。
まずは、必要なライブラリをインストールし、次に実際のガチャシミュレーションを行います。
以下にサンプルコードを示します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# 確率pで成功するガチャをN回まわす
p = 0.01 # 成功確率1%
N = 100 # ガチャをまわす回数
# 成功回数の確率分布を計算
x = np.arange(0, N+1)
y = binom.pmf(x, N, p)
# 可視化
plt.bar(x, y)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.title(f'{N}回のガチャにおける成功回数の分布')
plt.show()
このコードは、確率1%のガチャを100回まわしたときに何回成功するかの分布を可視化するものです。
結果として得られるグラフは、ガチャの排出確率に基づいた期待値を視覚的に理解する助けになります。
Pythonで二項分布を計算する方法
Pythonで二項分布を計算するには、`scipy.stats`ライブラリを利用します。
このライブラリには二項分布に関する関数が豊富に揃っており、特定の試行回数と成功確率に基づく計算が簡単に行えます。
例えば、成功確率が1%で100回の試行を行う場合の二項分布を計算するには、次のようにします。
from scipy.stats import binom n = 100 # 試行回数 p = 0.01 # 成功確率 # 確率質量関数を計算 x = range(n + 1) pmf = binom.pmf(x, n, p) print(pmf)
このコードは、各成功回数に対する確率を計算し、リストとして出力します。
このリストを用いることで、ガチャを100回まわしたときの結果を詳細に解析することができます。
ガチャ排出確率をPythonで可視化する手順
ガチャの排出確率を可視化するための手順は以下の通りです。
まず、Pythonと必要なライブラリをインストールします。
次に、二項分布を計算するコードを記述し、その結果をグラフとして可視化します。
これにより、ガチャの排出確率がどのように分布するかを直感的に理解することができます。
二項分布の理論とそのガチャへの応用
二項分布の理論は、成功確率が一定の独立した試行を複数回行った場合の成功回数の分布を表します。
この理論をガチャに応用することで、特定のアイテムが出る確率を予測することができます。
例えば、確率1%のアイテムを100回のガチャで狙う場合、二項分布を用いてその結果を予測し、プレイヤーがどの程度の回数で目的のアイテムを入手できるかを理解することが可能です。
Pythonでの二項分布の実装例とコード解説
Pythonで二項分布を実装する際の具体的なコード例を以下に示します。
まずは必要なライブラリをインストールし、次に実際のガチャシミュレーションを行います。
この例では、成功確率1%のガチャを100回まわした場合の成功回数をシミュレーションし、その結果を可視化します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# ガチャの設定
p = 0.01 # 成功確率1%
N = 100 # ガチャをまわす回数
# 二項分布の計算
x = np.arange
(0, N+1)
y = binom.pmf(x, N, p)
# 結果の可視化
plt.bar(x, y)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.title(f'{N}回のガチャにおける成功回数の分布')
plt.show()
このコードは、ガチャを100回まわした場合の成功回数の分布を可視化します。
これにより、プレイヤーはガチャの確率をより正確に理解し、戦略を立てることができます。
ガチャのシミュレーションとその結果の解釈
ガチャのシミュレーションを行うことで、実際のゲーム内でのガチャ結果を予測することができます。
シミュレーションの結果をグラフとして可視化することで、プレイヤーはどの程度の確率で目的のアイテムが得られるかを視覚的に理解できます。
これにより、ガチャの結果を予測し、効率的な戦略を立てることができます。
二項分布の基本概念とソーシャルゲームへの応用
二項分布は、確率論の基本的な概念の一つであり、成功または失敗の二つの結果しかない試行を複数回行った場合の成功回数の分布を表します。
ソーシャルゲームにおけるガチャの排出確率も、この二項分布の応用例といえます。
ガチャの結果は「当たり」か「ハズレ」の二つに分かれ、それが何回発生するかを計算するために二項分布が用いられます。
この分布を理解することで、プレイヤーはガチャを引く際の期待値や確率をより正確に予測することができ、また、運営側もゲームバランスの調整や確率の設定に役立てることができます。
二項分布とは何か:基礎から応用まで
二項分布は、成功確率が一定の独立した試行をN回行ったときに、成功回数がX回である確率を表す確率分布です。
具体的には、成功確率をp、試行回数をn、成功回数をkとしたとき、二項分布は次のように定義されます。
![]() ここで、
ここで、![]() は二項係数と呼ばれ、n回の試行からk回の成功を選ぶ組み合わせの数を表します。
は二項係数と呼ばれ、n回の試行からk回の成功を選ぶ組み合わせの数を表します。
この基礎知識をソーシャルゲームのガチャに適用することで、プレイヤーが特定のアイテムを引く確率を計算することが可能になります。
二項分布の数式とその解釈
二項分布の数式は、成功確率と試行回数に基づいて、特定の成功回数がどれだけの確率で発生するかを計算するものです。
例えば、成功確率が1%のガチャを100回引いた場合、そのうち1回成功する確率は次のように計算されます。
from scipy.stats import binom
# パラメータの設定
n = 100
p = 0.01
# 成功回数1回の確率を計算
prob = binom.pmf(1, n, p)
print(f'成功回数1回の確率: {prob:.4f}')
このコードは、成功回数が1回の場合の確率を計算し、結果を表示します。
このようにして、プレイヤーはガチャを引く際の具体的な確率を理解することができます。
二項分布がガチャに適用される理由
二項分布は、成功と失敗の二つの結果しかない試行を複数回行う場合に適用されます。
ガチャも同様に、「当たり」か「ハズレ」の二つの結果しかないため、二項分布が適用されます。
これにより、プレイヤーはガチャを引く回数と成功確率に基づいて、どれだけの確率で目当てのアイテムが得られるかを予測することができます。
ガチャ排出確率と二項分布の関係性
ガチャの排出確率と二項分布の関係性を理解することで、プレイヤーはガチャの結果をより正確に予測することができます。
例えば、確率1%のガチャを100回引いた場合の成功回数の分布を考えることで、プレイヤーはどの程度の確率で目的のアイテムが得られるかを理解することができます。
実際のゲームでの二項分布の適用例
実際のソーシャルゲームでは、ガチャの排出確率を二項分布に基づいて設定することが多く見られます。
例えば、レアアイテムの排出確率を低く設定し、それに基づいてプレイヤーがどれだけの回数ガチャを引く必要があるかを予測します。
このようにして、ゲームバランスを調整し、プレイヤーの課金意欲を高めることができます。
確率50%のコインを10回投げて表が出る確率の二項分布の例
確率50%のコインを10回投げたとき、表が出る回数の分布は典型的な二項分布の例です。
このシナリオを用いて二項分布の概念を説明することは、ガチャの排出確率を理解する上で非常に有益です。
例えば、コイン投げの結果がどのように分布するかを可視化することで、プレイヤーはガチャの結果がどのように分布するかを直感的に理解できます。
このような基礎的な例を通じて、二項分布の基本的な性質を学び、その後でより複雑なガチャの排出確率のシミュレーションに応用することができます。
コイン投げの二項分布の基本例
コイン投げの例では、成功確率が50%で10回の試行を行う場合の二項分布を考えます。
成功回数が0回から10回までの確率を計算し、その結果をグラフとして可視化します。
これにより、二項分布の基本的な概念を直感的に理解することができます。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# コイン投げの設定
p = 0.5 # 成功確率50%
N = 10 # 試行回数
# 二項分布の計算
x = np.arange(0, N+1)
y = binom.pmf(x, N, p)
# 結果の可視化
plt.bar(x, y)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.title(f'コイン投げにおける成功回数の分布({N}回投げた場合)')
plt.show()
このコードは、コインを10回投げた場合の成功回数の分布を可視化します。
これにより、プレイヤーは基本的な二項分布の概念を理解しやすくなります。
Pythonを使ったコイン投げシミュレーション
Pythonを使ってコイン投げのシミュレーションを行い、その結果を分析します。
このシミュレーションは、コインを10回投げたときに表が出る回数を1000回試行し、その結果を集計します。
import numpy as np
# シミュレーションの設定
p = 0.5 # 成功確率50%
N = 10 # 試行回数
trials = 1000 # シミュレーション回数
# シミュレーションの実行
results = np.random.binomial(N, p, trials)
# 結果の集計
(unique, counts) = np.unique(results, return_counts=True)
frequencies = counts / trials
# 結果の表示
for value, frequency in zip(unique,
frequencies):
print(f'成功回数: {value}, 確率: {frequency:.4f}')
このコードは、コインを10回投げるシミュレーションを1000回行い、その結果を集計して確率を計算します。
このようにして、シミュレーションを通じて二項分布の実際の挙動を観察することができます。
コイン投げの二項分布の可視化
シミュレーション結果をグラフとして可視化することで、二項分布の概念をより直感的に理解できます。
先ほどのシミュレーション結果を用いて、成功回数の分布をヒストグラムとして表示します。
import matplotlib.pyplot as plt
# ヒストグラムの作成
plt.hist(results, bins=range(0, N+2), density=True, align='left', rwidth=0.8)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.title('コイン投げシミュレーションの結果')
plt.show()
このコードは、コインを10回投げたときの成功回数の分布をヒストグラムとして表示します。
これにより、シミュレーション結果が二項分布に従うことを視覚的に確認できます。
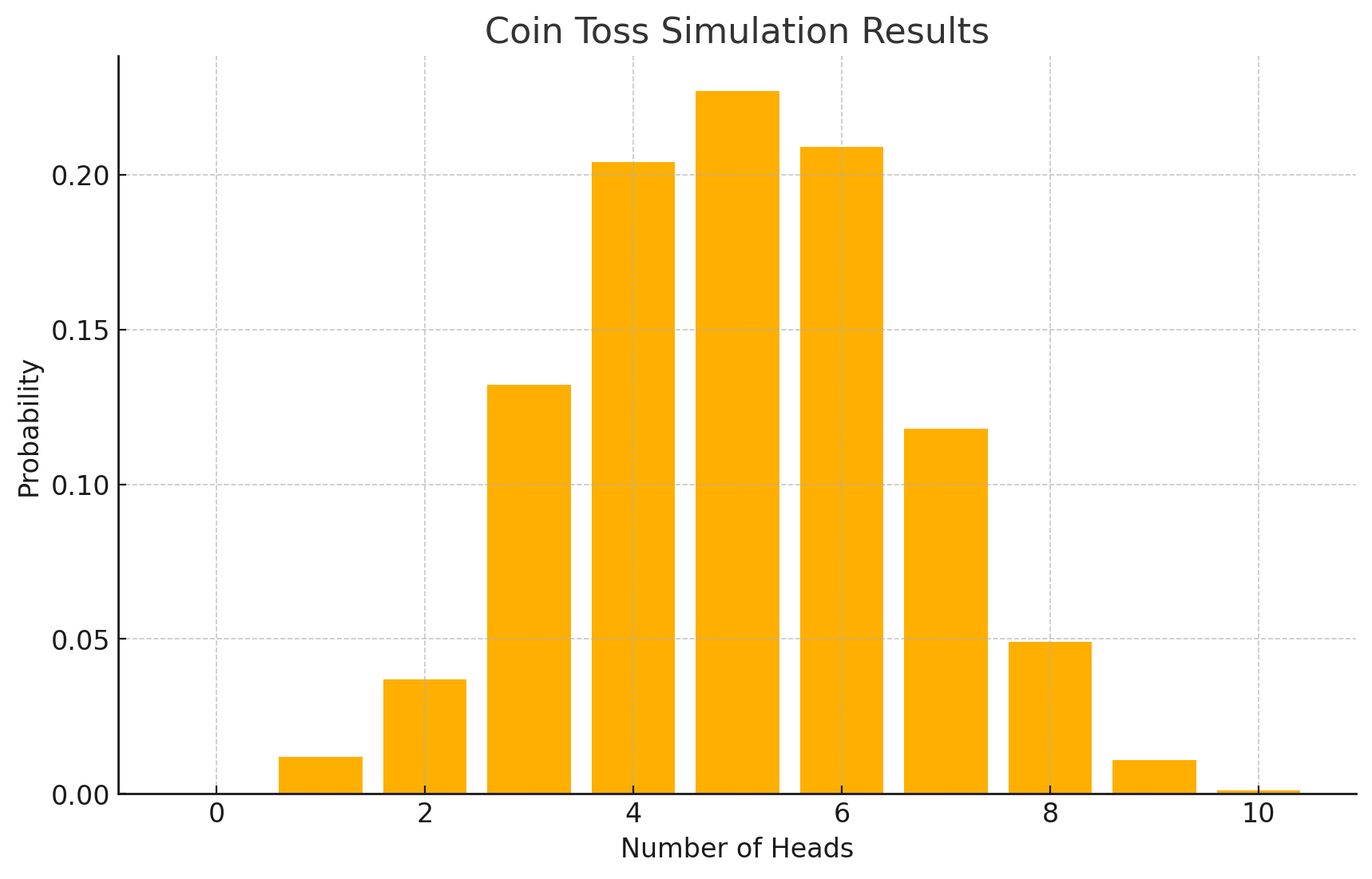
コイン投げ結果の解析とその意味
シミュレーション結果を解析することで、コイン投げの結果がどのように分布するかを理解できます。
例えば、成功回数が5回前後に集中していることから、確率50%の試行では成功回数が平均値に近づく傾向があることがわかります。
このような解析を通じて、二項分布の基本的な性質を学ぶことができます。
他の確率例との比較と考察
コイン投げ以外の例でも二項分布が適用されるシナリオを考えることで、二項分布の応用範囲を広げることができます。
例えば、ガチャの排出確率や他の確率問題においても同様の分布が見られるため、これらの例を比較することで、二項分布の汎用性を理解することができます。
確率1%の当たりのガチャを100回まわした場合の二項分布解析
確率1%のガチャを100回まわした場合の二項分布解析は、ガチャシステムの理解に役立ちます。
この例では、成功確率が非常に低いため、ガチャを複数回まわすことで当たりを引く確率を分析することが重要です。
プレイヤーがどの程度の回数で目当てのアイテムを入手できるかを予測することで、効率的なガチャ戦略を立てることができます。
確率1%のガチャとは?その基本概念
確率1%のガチャは、100回引いて1回成功する確率があるガチャのことです。
このような低確率のガチャは、レアアイテムや強力なキャラクターを入手するためのものであり、プレイヤーの課金意欲を高める要因となります。
しかし、その低確率ゆえに、多くのプレイヤーが期待値を理解し、戦略的にガチャを引くことが求められます。
Pythonでのガチャシミュレーションとその結果
Pythonを用いて確率1%のガチャを100回まわすシミュレーションを行い、その結果を解析します。
以下にサンプルコードを示します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# ガチャの設定
p = 0.01 # 成功確率1%
N = 100 # ガチャをまわす回数
# 二項分布の計算
x = np.arange(0, N+1)
y = binom.pmf(x, N, p)
# 結果の可視化
plt.bar(x, y)
plt.xlabel('成功回数')
plt.ylabel('確率')
plt.title(f'確率1%のガチャを100回まわした場合の分布')
plt.show()
このコードは、成功確率1%のガチャを100回まわしたときの成功回数の分布を可視化します。
これにより、プレイヤーは実際のガチャ結果を予測しやすくなります。
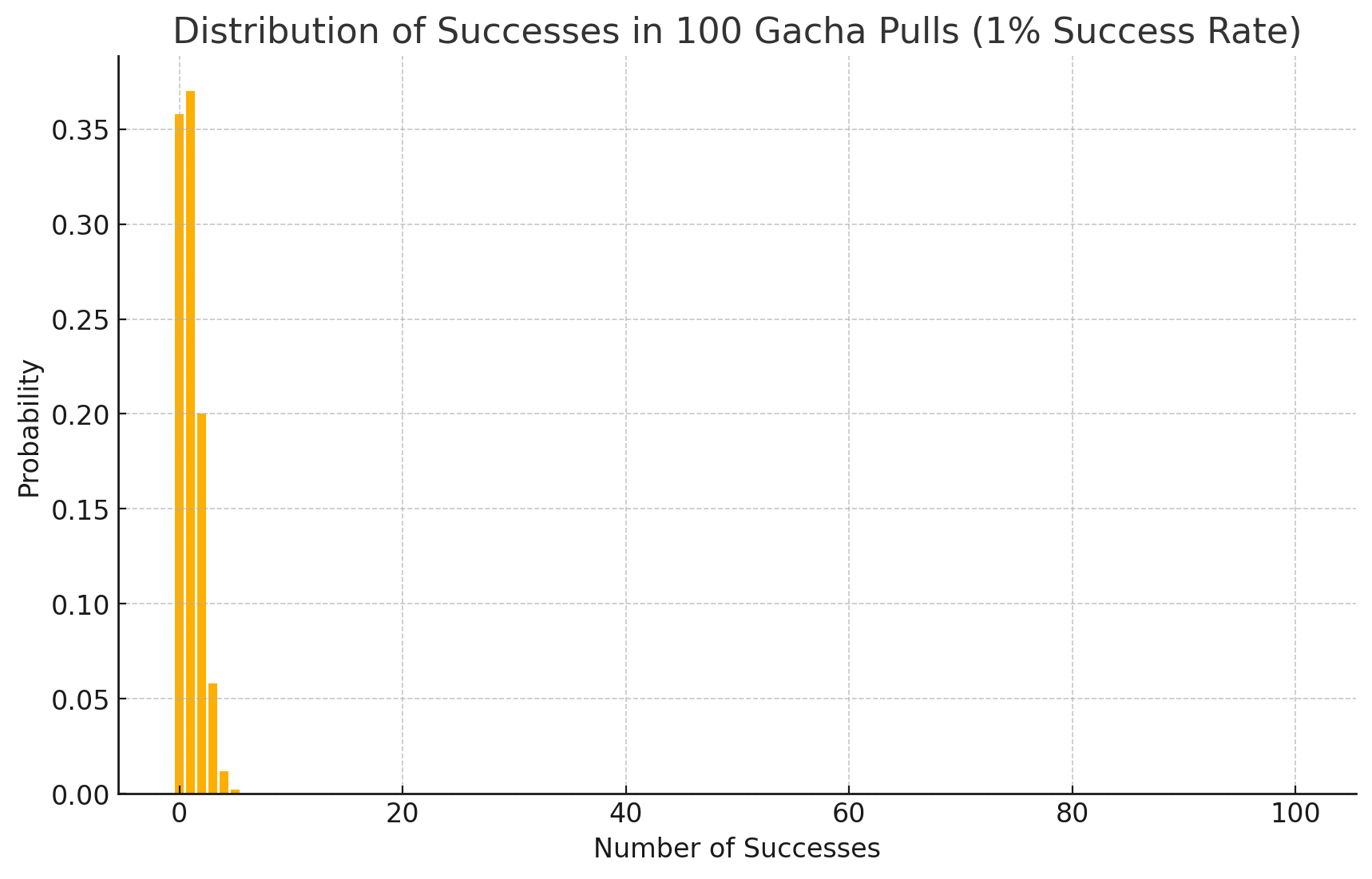
100回まわした場合の二項分布のグラフ化
確率1%のガチャを100回まわした場合の成功回数をグラフ化することで、どの程度の確率で当たりが出るかを視覚的に理解できます。
このグラフは、ガチャを引く回数と成功回数の関係を示し、プレイヤーがどのようにガチャを引くかの参考になります。
結果の解析と考察:期待値と現実の違い
シミュレーション結果を解析することで、期待値と現実の違いを理解できます。
例えば、確率1%のガチャを100回まわしても、必ずしも1回当たりが出るわけではありません。
このような解析を通じて、プレイヤーはガチャの結果に対する現実的な期待を持つことができます。
ガチャ排出確率を改善する方法と提案
ガチャの排出確率を改善するための方法として、運営側は確率を調整したり、保証機能を導入することが考えられます。
例えば、一定回数引いた後に必ず当たりが出るようにすることで、プレイヤーの不満を軽減し、満足度を向上させることができます。
確率1%のガチャを100回、200回、300回とまわした場合の結果比較
確率1%のガチャを100回、200回、300回とまわした場合の結果を比較することで、試行回数の増加が成功確率に与える影響を理解することができます。
この比較を通じて、プレイヤーはどの程度の回数で目的のアイテムを得られる可能性が高まるかを把握することができます。
複数回のガチャシミュレーションの準備と設定
まず、100回、200回、300回のガチャシミュレーションを行うための準備を行います。
各試行回数に対して成功確率を設定し、シミュレーションを実行します。
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import binom
# ガチャの設定
p = 0.01 # 成功確率1%
trials = [100, 200, 300] # ガチャをまわす回数
# シミュレーション結果の格納
results = []
for N in trials:
x = np.arange(0, N+1)
y = binom.pmf(x, N, p)
results.append((x, y))
# 結果の可視化
fig, axes = plt.subplots(len(trials), 1, figsize=(10, 15))
for ax, (x, y), N in zip(axes, results, trials):
ax.bar(x, y)
ax.set_xlabel('成功回数')
ax.set_ylabel('確率')
ax.set_title(f'確率1%のガチャを{N}回まわした場合の分布')
plt.tight_layout()
plt.show()
このコードは、100回、200回、300回のガチャシミュレーションを行い、それぞれの成功回数の分布を可視化します。
100回、200回、300回それぞれのシミュレーション結果
各シミュレーション結果を比較することで、試行回数の増加が成功確率にどのように影響するかを理解できます。
例えば、100回よりも200回、300回と試行回数が増えることで、成功回数の分布がどのように変化するかを視覚的に確認できます。
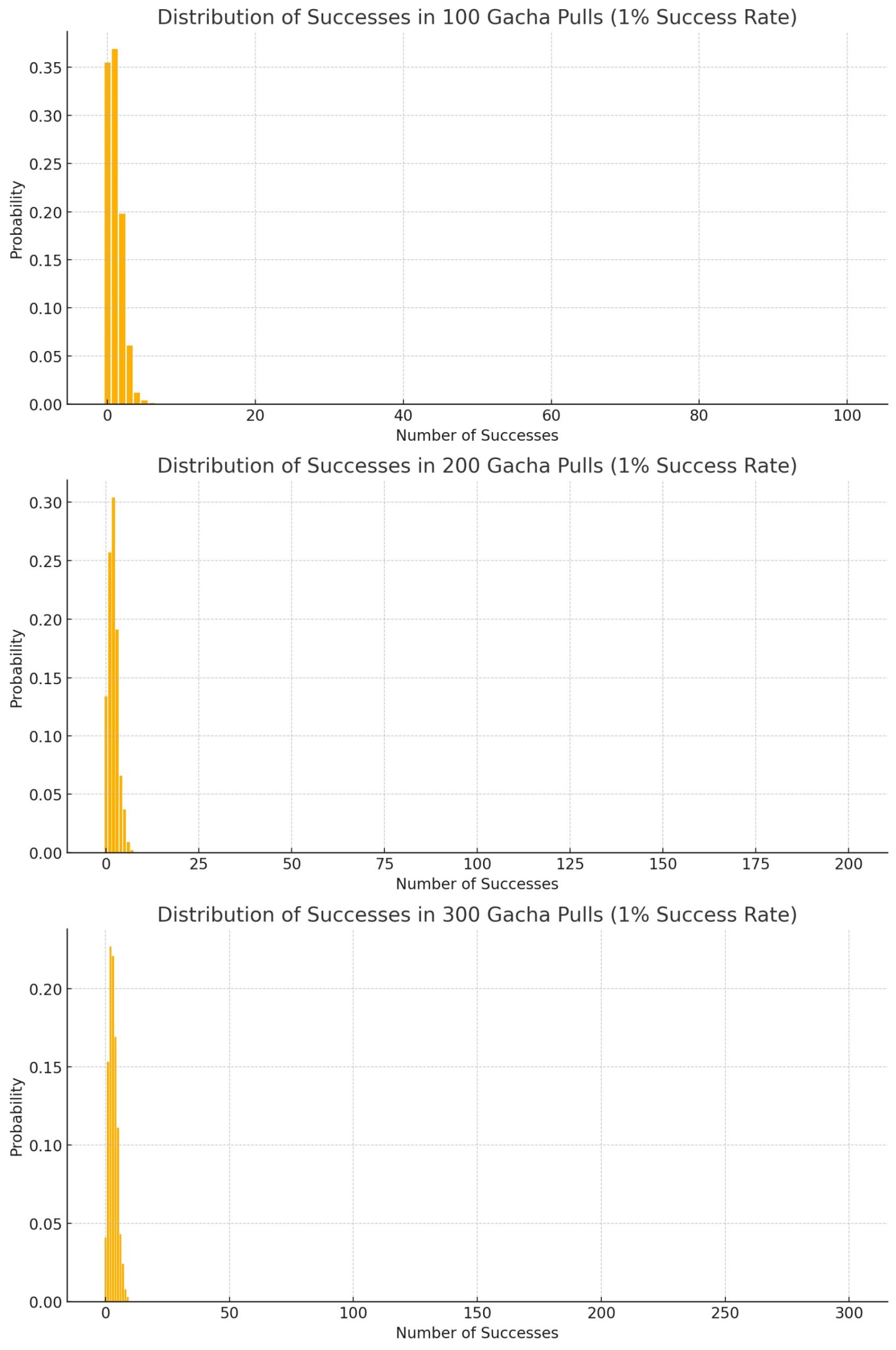
シミュレーション結果の可視化と比較
シミュレーション結果をグラフとして可視化することで、各試行回数における成功確率の違いを直感的に理解できます。
これにより、プレイヤーはどの程度の回数でガチャを引けば目的のアイテムが得られる可能性が高まるかを把握できます。
回数を増やすことによる期待値の変化
試行回数を増やすことで期待値がどのように変化するかを理解することは重要です。
例えば、100回のガチャでの期待値と200回、300回での期待値を比較することで、より多くのガチャを引くことの効果を確認できます。
結果から見えるガチャ戦略の提案
シミュレーション結果を基に、効率的なガチャ戦略を提案します。
例えば、一定回数引いた後に確率が上昇するイベントを活用する、特定のタイミングでガチャを引くなど、プレイヤーが効果的にガチャを引くための戦略を紹介します。





